06wk: 측도론 (2)

Author

최규빈

Published

April 11, 2023

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-y2r-mEbWKnTAC_8CN5HcGo

예비학습

약한조건, 약한정리, 강한조건, 강한정리

- 정리: 어떠한 조건을 만족하면, 어떠한 결론이 나온다.

결론: 우리가 원하는 것.
조건: 우리가 원하는 것을 얻기 위한 고난과정.

- 결론이 동일하다면 조건이 약할 수록 유리하다.

정리1: 수업에 온라인으로 참석하거나 오프라인으로 참석한다면 모두 출석으로 인정한다.
정리2: 수업에 오프라인으로 참석할때만 출석으로 인정한다.

정리2의 조건이 만족되면 정리1의 조건은 자동으로 만족된다. 따라서 정리2의 조건이 더 강한 조건이다. 조건이 강할수록 불리하므로 정리2가 더 불리하다.

- 조건이 동일하다면 결론이 강한 쪽이 유리하다.

정리1: 중간고사와 기말고사를 모두 응시한다면, B학점 이상이다.
정리2: 중간고사와 기말고사를 모두 응시한다면, A학점 이상이다.

정리2의 결론이 만족되면 정리1의 결론은 자동으로 만족되므로 정리2의 결론이 더 강하다. 결론은 강할수록 유리하므로 정리2가 더 유리하다.

쓸모없는 측도

- 세상엔 측도의 정의를 만족하지만 쓸모 없는 측도가 있다.

예시1: \({\cal F}\)의 모든 원소의 메져값은 0이다.
예시2: \({\cal F}\)의 모든 원소의 메져값은 무한대이다.

- 예시2와 같은 측도를 고려하고 싶지 않음 \(\Rightarrow\) 유한측도, 시그마유한측도의 개발

쓸모없는 가측공간

- 세상엔 쓸모없는 잴 수 없는 공간이 있다. (유의미한 측도를 주는게 불가능한 잴 수 있는 공간)

예시1: \({\cal F}= \{\emptyset, \Omega\}\)
예시2: \(\Omega =\mathbb{R}\) 일때 \({\cal F}=2^{\mathbb{R}}\) (르벡메져로 측정불가능함, 모든 원소의 메져를 0으로 잡으면 무모순으로 길이를 정의할 수는 있겠으나 무슨의미?)

- 예시2와 같은 \({\cal F}\)는 고려하고 싶지 않음 \(\Rightarrow\) \(\sigma({\cal A})\), 카라테오도리 확장정리의 고안.

유한측도, 시그마유한측도

- \(m\)이 잴 수 있는 공간 \((\Omega, {\cal F})\)에서의 측도라고 하자.

\(\forall A \in {\cal F}\), \(m(A) < \infty\) 이면 \(m\)을 유한측도라고 한다.¹
\(\exists A_1,A_2,\dots \in {\cal F}\) such that (1) \(\cup_{i=1}^{\infty}A_i = \Omega\) (2) \(\forall i \in \mathbb{N}:~ m(A_i)<\infty\) 이면 \(m\)을 시그마유한측도라고 한다.

¹ 사실 그냥 \(m(\Omega)<\infty\)라는 소리야

² \(A_1=\Omega\)로 잡으면 된다

- NOTE: 모든 확률측도는 유한측도이다. 모든 유한측도는 시그마유한측도이다.²

확률측도라는 것은 매우 강한 조건임
시그마유한측도라는 것은 확률측도보다 훨씬 약한 조건임

- 직관: 제 생각일 뿐이어요..

세상엔 측도의 정의는 만족하지만 쓸모없는 측도가 있다. (모든 원소를 쟀더니 0이더라, 모든 원소를 쟀더니 무한대더라)
그래서 모든 원소값에 무한대를 주는 측도는 인정하고 싶은 마음이 별로 없음. (하지만 측도의 정의는 만족)
그래서 그냥 유한측도만 생각하기로 했는데…

- 유한측도는 아니지만 시그마유한측도의 정의를 만족하는 경우 (엄청 중요해 보이는 예제들이 시그마유한측도잖아?)

르벡메져
카운팅메져: \(m\) is counting msr on \((\Omega, {\cal F})\) iff \(m(A) = \begin{cases} |A| & {\tt if}~ A~{\tt is~finite} \\ \infty & {\tt if}~A~{\tt is~infinite}\end{cases}\)

- 시그마유한측도의 느낌: 전체집합을 카운터블 유니온으로 커버하는 메져유한인 집합열이 1개만 있으면 된다.

(기억해둘만한 예시)

\((\mathbb{Z}, 2^{\mathbb{Z}})\) 를 잴 수 있는 공간이라고 하자. \(m\)을 공간 \((\mathbb{Z}, 2^{\mathbb{Z}})\)에서의 카운팅메져라고 하자.

집합열1

\(A_1=\mathbb{N}\)
\(A_2=\mathbb{N} \cup \{0\}\)
\(A_3=\mathbb{N} \cup \{-1,0\}\)
\(\dots\)

집합열2

\(B_1=\{0\}\)
\(B_2=\{0,1\}\)
\(B_3=\{-1,0,1\}\)
\(\dots\)

집합열1와 집합열2는

(1) \(\cup_{i=1}^{\infty}A_i=\mathbb{Z}\), (2) \(\forall i \in \mathbb{N}:~ m(A_i)=\infty\)
(1) \(\cup_{i=1}^{\infty}B_i=\mathbb{Z}\), (2) \(\forall i \in \mathbb{N}:~ m(B_i)<\infty\)

를 만족한다. 즉 집합열1은 전체집합을 카운터블 유니온으로 커버하지만 메져유한은 아니고, 집합열2는 전제집합을 카운터블 유니온으로 커버하고 메져유한이다. 집합열2의 존재로 인하여 \(m\)은 \((\mathbb{Z}, 2^{\mathbb{Z}})\)에서의 시그마유한측도가 된다.

확률공간

- \(P:{\cal F} \to [0,1]\) 가 잴 수 있는 공간 \((\Omega, {\cal F})\) 에서의 확률측도라면, \((\Omega, {\cal F}, P)\) 를 확률공간이라 선언할 수 있다.

- \((\Omega, {\cal F})\)가 잴수 있는 공간이라는 선언은 \({\cal F}\)가 \(\Omega\)에 대한 시그마필드라는 것이 내포되어 있다.

- \((\Omega, {\cal F}, P)\)가 확률공간이라는 선언에는

\({\cal F}\)는 \(\Omega\)에 대한 시그마필드이며,
\(P\)는 \((\Omega, {\cal F})\)에서의 확률측도임이 내포되어 있다.

- 교재의 언급 (p1) – 초록색부분

시그마유한측도공간

- \(m:{\cal F} \to [0,\infty]\)이 잴 수 있는 공간 \((\Omega, {\cal F})\)에서의 시그마유한측도라면, \((\Omega, {\cal F}, m)\)을 시그마유한측도공간이라 부른다.

- \((\Omega, {\cal F}, m)\)이 시그마유한측도공간이라는 선언에는

\({\cal F}\)는 \(\Omega\)에 대한 시그마필드이며,
\(m\)는 \((\Omega, {\cal F})\)에서의 시그마유한측도임이 내포되어 있다.

Generating \(\sigma\)-field

state

- Thm (귀찮아서 만든 이론1): 모든 \({\cal A} \subset 2^{\Omega}\) 에 대하여 smallest \(\sigma\)-field containing \({\cal A}\), 즉 \(\sigma({\cal A})\)는 존재한다.

그리고 당연히 smallest 조건에 의에서 유일성이 보장됨

증명을 위한 준비학습

- 이론: (\(\star\)) 임의의 인덱스 집합 \(I\neq\emptyset\)를 고려하자. 여기에서 \(I\)는 uncountable set일 수도 있다. 아래의 사실에 증명하라.

\({\cal F}_i\)가 모두 시그마필드라면, \(\cap_{i \in I}{\cal F_i}\) 역시 시그마필드이다.

(증명)

편의상 \({\cal F}= \cap_{i \in I} {\cal F}_i\) 라고 하자. \({\cal F}\)가 시그마필드임을 보이기 위해서는

\(A \in {\cal F} \Rightarrow A^c \in {\cal F}\)
\(A_1,A_2 \dots \in {\cal F} \Rightarrow \cup_{i}A_i \in {\cal F}\)

만 보이면 된다. (이럴때는 전체집합 조건하나를 빼는게 유리하다)

1번체크

\(A \in {\cal F} \Rightarrow \forall i: A \in {\cal F}_i \Rightarrow \forall i: A^c \in {\cal F}_i \Rightarrow A^c \in {\cal F}\)

2번체크

\(A_1,A_2,\dots \in {\cal F} \Rightarrow \forall i: A_1,A_2,\dots \in {\cal F}_i \Rightarrow \forall i: \cup_jA_j \in {\cal F}_i \Rightarrow \cup_jA_j \in {\cal F}\)

증명

- Thm (귀찮아서 만든 이론1): 모든 \({\cal A} \subset 2^{\Omega}\) 에 대하여 smallest \(\sigma\)-field containing \({\cal A}\), 즉 \(\sigma({\cal A})\)는 존재한다.

그리고 당연히 smallest 조건에 의해 유일성이 보장됨

(증명)

\({\cal A}\)를 포함하는 모든 시그마필드를 구하고 그걸 교집합하여 결과를 \({\cal F}\)라고 하자. 아래의 사실은 자명하게 성립한다.

시그마필드의 교집합은 시그마필드이므로 \({\cal F}\)는 시그마필드이다.
교집합을 하면 할수록 집합은 작아지므로 \({\cal F}\)는 위에서 구한 시그마필드중에서 가장 작다.
\({\cal F}\)는 \({\cal A}\)를 포함한다.

따라서 \({\cal F}\)는 (\({\cal A}\)를 포함하는 모든 시그마필드를 교집합하여 얻은 집합) \({\cal A}\)를 포함하는 가장 작은 시그마필드가 된다.

- 아래는 교재의 언급 (p3)

Dynkin’s \(\pi\)-\(\lambda\) theorem

state

- Thm: 딘킨의 \(\pi-\lambda\) 정리 ver1. (\(\star\))

\({\cal P}\)가 파이시스템이면 \(l({\cal P})=\sigma({\cal P})\)이다.

증명을 위한 준비학습

- 이론: 임의의 인덱스 집합 \(I\neq\emptyset\)를 고려하자. 여기에서 \(I\)는 uncountable set일 수도 있다. 아래의 사실이 성립한다.

\({\cal F}_i\)가 모두 시그마필드라면, \(\cap_{i \in I}{\cal F_i}\) 역시 시그마필드이다.
\({\cal A}_i\)가 모두 시그마링, \(\cap_{i \in I}{\cal A_i}\) 역시 시그마링이다.
\({\cal A}_i\)가 모두 알지브라라면, \(\cap_{i \in I}{\cal A_i}\) 역시 알지브라이다.
\({\cal A}_i\)가 모두 링이라면, \(\cap_{i \in I}{\cal A_i}\) 역시 링이다.
\({\cal A}_i\)가 모두 람다시스템이라면, \(\cap_{i \in I}{\cal A_i}\) 역시 람다시스템이다.

세미알지브라, 세미링, 파이시스템은 성립안함.

- 예제1: 아래를 고려하자.

\(\Omega = \{1,2,3,4\}\)
\({\cal A}_1 = \{\emptyset, \{1\}, \{2,3\}, \{4\}, \Omega\}\)
\({\cal A}_2 = \{\emptyset, \{1\}, \{2\}, \{3,4\}, \Omega\}\)

\({\cal A}_1, {\cal A}_2\)는 모두 세미알지브라이다. 하지만 \({\cal A}_1 \cap {\cal A}_2 = \{\emptyset, \Omega, \{1\}\}\)은 세미알지브라가 아니다.

이 예제에서 세미알지브라를 세미링으로 바꾸고 읽어도 성립함.

- 예제2: 아래를 고려하자.

\(\Omega=\{H,T\}\)
\({\cal A}_1 = \{\{H\}\}\)
\({\cal A}_2 = \{\{T\}\}\)

\({\cal A}_1, {\cal A}_2\)는 모두 파이시스템이다. 하지만 \({\cal A}_1 \cap {\cal A}_2 = \emptyset\)은 파이시스템이 아니다.

- 이론: 임의의 \({\cal A}\)에 대하여 아래는 존재한다.

\({\cal A}\)를 포함하는 가장 작은 시그마필드, \(\sigma({\cal A})\)
\({\cal A}\)를 포함하는 가장 작은 시그마링
\({\cal A}\)를 포함하는 가장 작은 알지브라
\({\cal A}\)를 포함하는 가장 작은 링
\({\cal A}\)를 포함하는 가장 작은 람다시스템, \(l({\cal A})\)

- 참고: “\({\cal A}\)를 포함하는 가장 작은 세미링”, 혹은 “\({\cal A}\)를 포함하는 가장 작은 세미알지브라”와 같은 것은 존재하지 않음.

- 예제3: 아래를 고려하자.

\(\Omega = \{1,2,3,4\}\)
\({\cal A} = \{\emptyset, \Omega, \{1\}\}\)

이때 \({\cal A}\)를 포함하는 가장 작은 세미알지브라가

\[{\cal A}_1 = \{\emptyset, \Omega, \{1\}, \{2,3,4\}\}\]

라고 주장할 수는 없음. 왜냐하면

\[{\cal A}_2 = \{\emptyset, \Omega, \{1\}, \{2\},\{3\},\{4\}\}\]

역시 \({\cal A}\)를 포함하는 세미알지브라이지만 \({\cal A}_1 \not \subset {\cal A}_2\)이므로.

- 이론: \({\cal P}\)가 파이시스템이라고 하자. 아래가 성립한다.

\({\cal P}\)를 포함하는 가장 작은 시그마필드는 그 자체로 파이시스템이다. (즉 \(\sigma({\cal P})\)는 파이시스템이다)
\({\cal P}\)를 포함하는 가장 작은 시그마링은 그 자체로 파이시스템이다.
\({\cal P}\)를 포함하는 가장 작은 알지브라는 그 자체로 파이시스템이다.
\({\cal P}\)를 포함하는 가장 작은 링은 그 자체로 파이시스템이다.
\({\cal P}\)를 포함하는 가장 작은 람다시스템은 그 자체로 파이시스템이다?? (즉 \(l({\cal P})\)는 파이시스템이다?)

- 1-4는 자명한데, 5는 자명하지 않다. 하지만 성립한다. (5의 증명은 복잡함. 그냥 암기하자.)

- 이론: \({\cal A}\)가 람다시스템이다. \(\Rightarrow\) (\({\cal A}\)는 시그마필드이다. \(\Leftrightarrow\) \({\cal A}\)는 파이시스템이다.)

(증명) 아래의 표를 살펴보면 간단하게 증명가능하다.

	\(A \cap B\)	\(\emptyset\)	\(A-B\)	\(\cup_iA_i=\uplus_i B_i\)	\(\Omega\)	\(A^c\)	\(A\cup B\)	\(\cup_{i=1}^{\infty}A_i\)	\(\uplus_{i=1}^{\infty}B_i\)	\(\cap_{i=1}^{\infty}A_i\)
\(\pi\)-system	\(O\)	\(X\)	\(X\)	\(X\)	\(X\)	\(X\)	\(X\)	\(X\)	\(X\)	\(X\)
\(\lambda\)-system	\(X\)	\(O\)	\(\Delta'\)	\(X\)	\(O\)	\(O\)	\(X\)	\(X\)	\(O\)	\(X\)
\(\sigma\)-field	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)	\(O\)

증명

(증명)

\(l(\cal P) \subset \sigma({\cal P})\) 임을 보이고, \(l(\cal P) \supset \sigma({\cal P})\) 임을 보이면된다.

“\(\subset\)”: 당연하다.³

³ 직접 만들어봐, 시그마필드가 당연히 조건이 더 복잡하므로 이거저것 추가할 것이 많음

“\(\supset\)”: \(l({\cal P})\)가 시그마필드임을 보이면 자동으로 \(l({\cal P}) \supset \sigma({\cal P})\)임이 보여진다.

\(l({\cal P})\)이 시그마필드임은 아래를 조합하면 간단히 증명된다.

파이시스템 \({\cal P}\)를 포함하는 가장 작은 람다시스템 \(l({\cal P})\)은 그 자체로 파이시스템이다.
\({\cal A}\)가 람다시스템이다. \(\Rightarrow\) (\({\cal A}\)는 시그마필드이다. \(\Leftrightarrow\) \({\cal A}\)는 파이시스템이다.)

- 생각의 시간

시그마필드(=잴 수 있는 집합의 모임)을 만들기 위해서는, 그 모임(=collection)이 파이시스템이면서 동시에 람다시스템임을 보이면 된다.
딘킨의 정리는 적당한 파이시스템을 만들고 그것을 통하여 잴 수 있는 집합의 모임을 확률의 공리에 맞게만 설정한다면, 그것이 시그마필드가 된다는 것을 보이는 것이다.

- 제 생각

메져가 “선분의 길이”를 일반화 하는 개념이라 생각한다면 파이시스템에서 시작하여 시그마필드로 확장하는 것이 자연스럽다.
메져가 “확률”을 일반화하는 개념이라 생각한다면 람다시스템에서 시작하는게 자연스럽다.⁴
딘킨의 \(\pi-\lambda\) 정리는 두 흐름을 합치는 정리이다.

⁴ 딘킨도 이렇게 생각하지 않았을까

딘킨의 \(\pi-\lambda\) 정리 ver2.

- 이론: 딘킨의 \(\pi-\lambda\) 정리 ver2.

\({\cal P}\)가 파이시스템이고 \({\cal L}\)이 \({\cal P}\)를 포함하는 람다시스템이라면 \(\sigma({\cal P}) \subset {\cal L}\)이다.

(설명)

Durret에 나온 딘킨의 \(\pi-\lambda\) thm 이다. 굉장히 불친절한 편인데, ver2가 증명되면 ver1은 자명하게⁵ 임플라이 되므로 ver2를 대신 state한 것이다.

⁵ 솔직히 그렇게 안자명해

ver2가 ver1를 임플라이 하는 이유: ver1의 \(l({\cal P}) \subset \sigma({\cal P})\)은 당연하고 \(l({\cal P}) \supset \sigma({\cal P})\)만 보이면 되는데, 이미 \(\sigma({\cal P}) \subset {\cal L}\)임을 보였으므로 \(l({\cal P})\)의 정의에 의하여 \({\cal L} \supset l({\cal P}) \supset \sigma({\cal P})\)이 성립한다.

- 교재의 언급 (p 456)

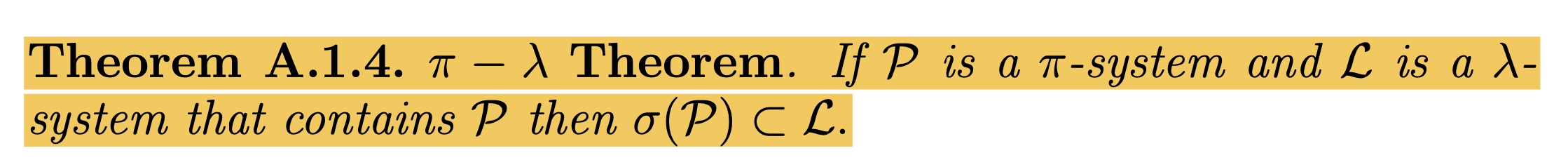
파이시스템에서의 확장이론 (확률버전)

state

- 귀찮아서 만든 이론2: 운이 좋다면, \({\cal A}\) 에서 확률의 공리를 만족하는 적당한 함수 \(\tilde{P}:{\cal A} \to [0,1]\)를 \((\Omega, \sigma({\cal A}))\) 에서의 확률측도 \(P\)로 업그레이드 할 수 있으며 업그레이드 결과는 유일하다.

- 귀찮아서 만든 이론2는 (1) 업그레이드가 가능하냐 (2) 그 업그레이드가 유일하냐 를 따져야하는데 이중 유일성만을 따져보자.

- Thm: \((\Omega, \sigma({\cal A}), P)\)를 확률공간이라고 하자. 여기에서 \({\cal A}\)는 파이시스템이라고 가정하자. 그렇다면 확률측도 \(P:\sigma({\cal A}) \to [0,1]\)의 값은 \(P: {\cal A} \to [0,1]\)의 값에 의하여 유일하게 결정된다.

\({\cal A}\)가 파이시스템이라면, \({\cal A}\)에서는 agree하지만 \(\sigma({\cal A})\)에서는 agree하지 않는 확률측도 \(P:\sigma({\cal A}) \to [0,1]\)는 존재할 수 없다는 의미이다.

활용예제 (\(\star\))

- 아래의 이론을 이해하기 위한 예제들을 살펴보자.

이론: \((\Omega, \sigma({\cal A}), P)\)를 확률공간이라고 하자. 여기에서 \({\cal A}\)는 파이시스템이라고 가정하자. 그렇다면 확률측도 \(P:\sigma({\cal A}) \to [0,1]\)의 값은 \(P: {\cal A} \to [0,1]\)의 값에 의하여 유일하게 결정된다.

(예제1) – 4주차에서 했던 예제에요

- \(\Omega=\{1,2,3,4\}\)이라고 하고 \({\cal A} = \{\emptyset, \{1\},\{2\},\{3,4\},\Omega\}\) 라고 하자.

- \({\cal A}\)는 파이시스템이다.

- 아래표의 왼쪽의 \(P\)와 같은 확률 측도를 고려하자.

	\(P\)	\(P'\)
\(\emptyset\)	\(0\)	\(0\)
\(\{1\}\)	\(\frac{1}{4}\)	\(\frac{1}{4}\)
\(\{2\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(\{3,4\}\)	\(\frac{1}{4}\)	\(\frac{1}{4}\)
\(\Omega\)	\(1\)	\(1\)
\(-\)	\(-\)	\(-\)
\(\{1,2\}\)	\(\frac{3}{4}\)	\(\frac{3}{4}\) 이 아닐 수 있어?
\(\{1,3,4\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\) 이 아닐 수 있어?
\(\{2,3,4\}\)	\(\frac{3}{4}\)	\(\frac{3}{4}\) 이 아닐 수 있어?

\({\cal A}\)에서는 \(P\)와 그 값이 같지만 \(\sigma({\cal A})-{\cal A}\)에서는 다른값을 가질 수도 있는 \((\Omega, \sigma({\cal A}))\) 에서의 확률측도 \(P'\)는 존재하지 않는다.

즉 \({\cal A}\)가 파이시스템이라면, \((\Omega,\sigma({\cal A}))\)에의 모든 확률측도 \(P\)는 \({\cal A}\)에서의 값만 define하면 나머지 \(\sigma({\cal A})-{\cal A}\)에서의 값은 유니크하게 결정된다.

- 이 이론에 대한 짧은 생각

생각1: 일단 \((\Omega,\sigma({\cal A})\)에서의 확률측도 \(P\)의 존재성은 가정하고 들어간다. 즉 “존재한다면 유일하다”는 의미이지, “유일하게 존재한다”의 의미는 아니다.
생각2: 따라서 이 정리는 “\({\cal A}\)가 파이시스템일 경우, 함수 \(\tilde{P}:{\cal A} \to [0,1]\)가 \((\Omega,\sigma({\cal A}))\)에서의 확률측도 \(P\)로 업그레이드가 가능하다면 그 결과는 유일하다” 정도로 해석할 수 있다.

(예제2) – 이것도 4주차에서 했던 예제입니다.

- \(\Omega=\{1,2,3,4\}\) 이라고 하고 \({\cal A} = \{\emptyset, \{1,2\},\{2,3\}, \Omega\}\) 라고 하자.

- 여기에서 \({\cal A}\)는 파이시스템이 아니다. 따라서 \({\cal A}\)에서의 값은 agree하지만 \((\Omega, \sigma({\cal A}))\)에서 agree하지 않는 서로 다른 확률측도가 존재할 수 있다.

	\(P_1\)	\(P_2\)
\(\emptyset\)	\(0\)	\(0\)
\(\{1,2\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(\{2,3\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(\Omega\)	\(1\)	\(1\)
\(-\)	\(-\)	\(-\)
\(\{1\}\)	\(0\)	\(\frac{1}{2}\)
\(\{2\}\)	\(\frac{1}{2}\)	\(0\)
\(\{3\}\)	\(0\)	\(\frac{1}{2}\)
\(\{4\}\)	\(\frac{1}{2}\)	\(0\)
\(\{1,3\}\)	\(0\)	\(1\)
\(\{1,4\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(\{2,4\}\)	\(1\)	\(0\)
\(\{3,4\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(\{2,3,4\}\)	\(1\)	\(\frac{1}{2}\)
\(\{1,3,4\}\)	\(\frac{1}{2}\)	\(1\)
\(\{1,2,4\}\)	\(1\)	\(\frac{1}{2}\)
\(\{1,2,3\}\)	\(\frac{1}{2}\)	\(1\)

- 만약에 이 예제에서 \({\cal A}\)를 아래와 같이 수정한다면

\[{\cal A}=\{\emptyset, \{1,2\}, \{2,3\}, \{2\}\}\]

이번에는 \({\cal A}\)는 파이시스템이 된다. 따라서 이 경우 \((\Omega, \sigma({\cal A}))\)에서의 모든 확률측도 \(P\)는 \({\cal A}\)의 값에 의하여 유일하게 결정된다.

(예제3)

- \(\Omega=\{H,T\}\) 이라고 하고 \({\cal A} = \{\{H\}\}\) 라고 하자.

- 여기에서 \({\cal A}\)은 파이시스템이므로 가측공간 \((\Omega,\sigma({\cal A}))\)에서 정의가능한 모든 확률측도 \(P\)는 \({\cal A}\)에서의 값으로만 정의해도 무방하다.⁶

⁶ 그래도 유일하게 결정되니까

(예제4) – 통계학과라서 행복해

- \(\Omega=\{a,b\}\) 이라고 하고 \({\cal A} = \{\{a\}\}\) 라고 하자.

- 여기에서 \({\cal A}\)은 파이시스템이다.

- 가측공간 \((\Omega,\sigma({\cal A}))\)에서 정의가능한 모든 확률측도 \(P\)는 \({\cal A}\)에서의 값으로 유일하게 결정된다.

- 그렇지만 가측공간 \((\Omega,\sigma({\cal A})\)에서 정의가능한 “측도” \(m\)은 \({\cal A}\)에서의 값으로 유일하게 결정되지 않는다.⁷

⁷ 그렇지만 우리가 알바는 아님

	\(m_1\)	\(m_2\)
\(\{a\}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)
\(-\)	\(-\)	\(-\)
\(\emptyset\)	\(0\)	\(0\)
\(\{b\}\)	\(\frac{1}{2}\)	\(1\)
\(\Omega\)	\(1\)	\(\frac{3}{2}\)

증명

- 아래의 이론에 대한 증명

Thm: \((\Omega, \sigma({\cal A}), P)\)를 확률공간이라고 하자. 여기에서 \({\cal A}\)는 파이시스템이라고 가정하자. 그렇다면 확률측도 \(P:\sigma({\cal A}) \to [0,1]\)의 값은 \(P: {\cal A} \to [0,1]\)의 값에 의하여 유일하게 결정된다.

증명 (확률측도라는 가정을 추가하여 교재의 버전을 살짝 쉽게 만듬)

LET

\((\Omega, \sigma({\cal A}))\) 는 잴 수 있는 공간임.
\(P_1,P_2\)는 \((\Omega, \sigma({\cal A}))\)에서의 확률측도임.
\(P_1,P_2\)는 “\(\forall A \in {\cal A}: P_1(A)=P_2(A)\)”를 만족함.

전략: 잴 수 있는 공간 \((\Omega, \sigma({\cal A}))\) 에서의 두 측도 \(P_1\), \(P_2\)가 \({\cal A}\)에서는 일치하지만 \(\sigma({\cal A})-{\cal A}\)에서는 일치하지 않는 경우를 찾으려 해보고, 그것이 불가능함을 보이자.

LET: \(\tilde{\cal D}=\{B \in \sigma({\cal A}): P_1(B) \neq P_2(B)\}\)

ISTST: \(\tilde{\cal D} =\emptyset\)

ISTST: \({\cal D} = \{B \in \sigma({\cal A}): P_1(B) = P_2(B) \} = \sigma({\cal A})\)

ISTST: (1) \({\cal D} \subset \sigma({\cal A})\) (2) \({\cal D} \supset \sigma({\cal A})\)

ISTST: \({\cal D} \supset \sigma({\cal A})\)

NOTE: IF (1) \({\cal D}\) is containing \({\cal A}\) (2) \({\cal D}\) is \(\lambda\)-system, THEN we can say \({\cal D} \supset \sigma({\cal A})=l({\cal A})\)

ISTST: (1) \({\cal A} \subset {\cal D}\) (2) \({\cal D}\) is \(\lambda\)-system.

ISTST: 1. \(\Omega \in {\cal D}\) 2. \(A,B \in {\cal D}, A\subset B\) \(\Rightarrow\) \(B-A \in {\cal D}\) 3. \(\forall B_1,B_2,\dots, \in {\cal D}\), \(\uplus_{i=1}^{\infty} B_i \in {\cal D}\)

CHECK 1: \(P_1(\Omega) = P_2(\Omega)\)

CHECK 2: \(P_1(B-A) = P_1(B)-P_1(A) = P_2(B) - P_2(A) = P_2(B-A)\)

CHECK 3: \(P_1(\uplus_{i=1}^{\infty} B_i)=P_1(B_1)+P_1(B_2)\dots = P_2(B_1)+P_2(B_2) +\dots = P_2(\uplus_{i=1}^\infty B_i)\)

- 보충노트

supp_6wk.pdf